이번 포스트에서는 앞에서 배운 KLD와 JSD를 이용하여 GAN에 대해 조금 더 수학적으로 파고 들어 보겠습니다. GAN은 단순히 이미지를 생성하는 알고리즘이 아닙니다. 주어진 데이터의 분포를 파악하고, 이렇게 파악한 결과로 학습한 데이터들과 유사한 데이터를 만들어낼 수 있게끔 하는 학습 알고리즘입니다. 여기서 주목할 점은 데이터의 분포를 파악한다는 점입니다. 어떻게 해서 파악할까요? 본문에서 알아보도록 하겠습니다.
- 선수 지식: 이 포스트를 이해하기 위해서는 KL Divergence & Jensen-Shannon Divergence에 대한 지식이 필요합니다.
- 참고 논문: Generative Adversarial Nets
분포를 파악한다??
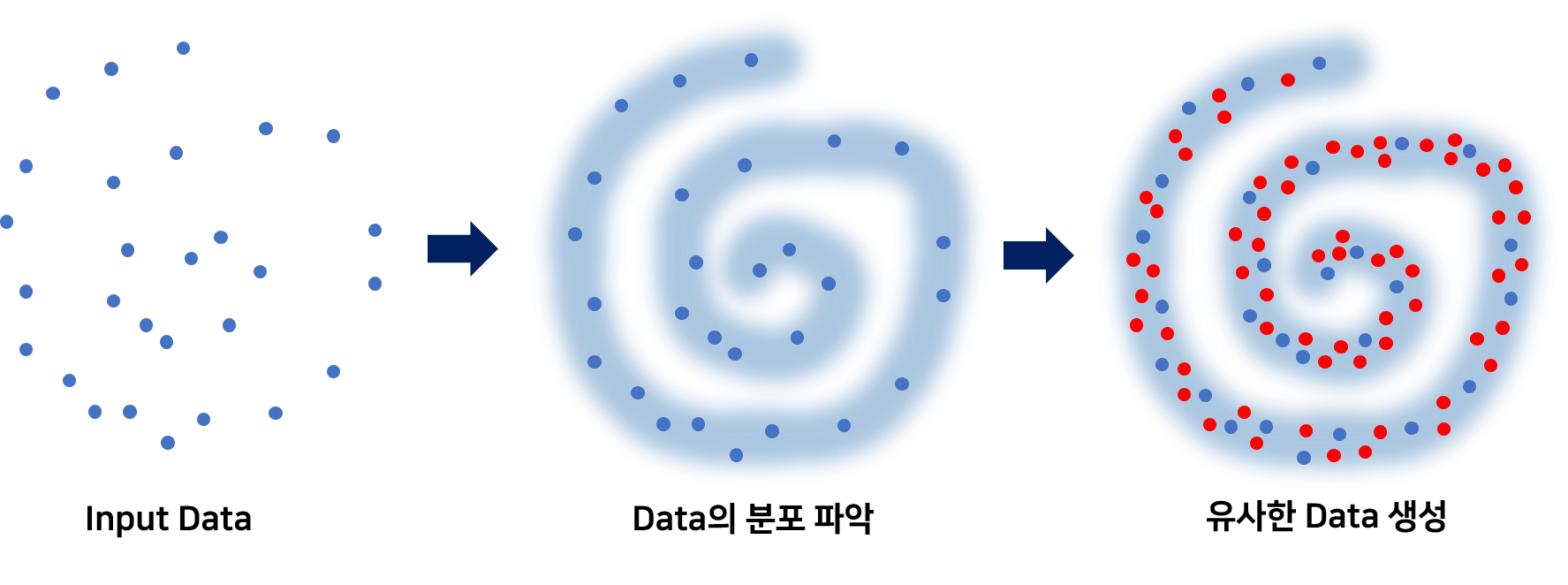
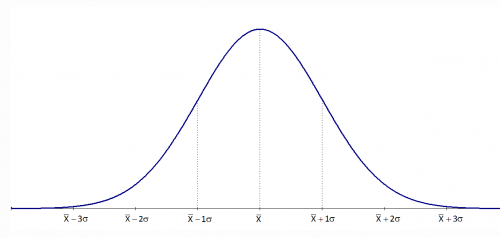
GAN은 단순히 데이터를 생성해 내는 알고리즘이 아니다. 주어진 데이터의 분포를 파악하고, 이렇게 파악한 결과로 학습한 데이터들과 유사한 데이터를 만들어낼 수 있게끔 하는 학습 알고리즘이다. Figure 1과 같이 주어진 데이터가 어떻게 생겼는지를 학습을 통해 먼저 파악한 후, 이렇게 학습된 내용을 바탕으로 주어진 데이터와 유사한 데이터들을 생성해낼 수 있게 되는 알고리즘인 것이다. 여기서 말하는 데이터의 분포는 바로 데이터의 확률 분포(Probability Distribution)이다. 확률 분포는 Random Variable X가 어떤 값을 가질 확률이 높은지를 나타낸 일종의 Map이다. Figure 2는 대표적인 확률분포인 Gaussian Distribution이다.
결국 GAN은 주어진 데이터의 확률 분포를 예측하는 모델이다. 확률 분포를 예측한다라… 분명 떠오르는 것이 있다. 앞에서 배운 Jensen-Shannon Divergence의 경우 두 확률 분포의 유사성을 판별해주는 척도중에 하나다. 그렇다면 GAN이 주어진 데이터의 실제 확률 분포와 GAN이 예측한 확률 분포 사이의 Jensen-Shannon Divergence를 최소화 하는 알고리즘이라는 것인가? 결론부터 말하면 그렇다. 그리고 우리는 이 사실을 간단한 수학적인 과정을 통해 증명해 보도록 할 것이다.
Discriminator의 최적화
GAN의 포스팅에서 살펴봤듯이, GAN 알고리즘은 다음 Object Function의 Min-Max Problem으로 귀결된다.
$$\min_ G \max_ D \{ \log(D(x)) + \log(1-D(G(z))) \}$$
이 식은 일반적인 $x$와 $z$에 대한 식인데, 실제로는 $x$는 우리가 가진 Dataset으로부터 sampling되고 z 또한 random한 방식으로 sampling된다. sampling에 따른 불확실성을 반영하기 위해, 우리는 식에 기댓값을 적용시키게 된다.
이 식을 바탕으로 G와 D를 최적화시킬 것인데, 먼저 G가 고정되었다고 가정하고 D를 최적화시켜보도록 하자.
$$\min_ G \max_ D [ V(G, D) ]$$
$$V(G, D) = E_ {x \sim p_ {data} (x)} [ \log(D(x)) ] + E_ {z \sim p_ {z} (z)} [ \log(1-D(G(z))) ] $$
이 때, $E_ {z \sim p_ {z} (z)} [ \log(1-D(G(z))) ]$에서 우리가 실제 sampling을 통해 관찰하는 대상은 $z$가 아니라 $G(z)$이므로, $y = G(z)$에 대하여 다음과 같이 쓸 수 있다.
$$E_ {z \sim p_ {z} (z)} [ \log(1-D(G(z))) ] = E_ {y \sim p_ {g} (y)} [ \log(1-D(y)) ] $$
$$V(G, D) = E_ {x \sim p_ {data} (x)} [ \log(D(x)) ] + E_ {y \sim p_ {g} (y)} [ \log(1-D(y)) ]$$
그러므로 기댓값의 정의에 의해 다음과 같이 계산이 가능하다.
$$V(G, D) = \int_ {x} {p_ {data} (x) \log(D(x)) dx} + \int_ {y} {p_ {g} (y) \log(1-D(y)) dy}$$
$$ \qquad = \int_ {x} {p_ {data} (x) \log(D(x)) + p_ {g} (x) \log(1-D(x)) dx}$$
$D$에 관한 미분을 통해 $V(D,G)$가 최댓값을 갖는 점을 구하면 $D^*_ {G} (x) = \frac{p_ {data} (x)}{p_ {data} (x) + p_ {g} (x)}$ 라는 사실을 쉽게 알 수 있다.
Generator의 최적화
Discriminator를 최적화하였으니, $D=D^*$로 고정하고 Generator를 최적화 하도록 할 것이다. 그러기 위해서 식을 살짝 변형해보도록 하자.
$$V(G,D^*) = E_ {x \sim p_ {data} (x)} [ \log(D ^ * (x)) ] + E_ {x \sim p_ {g} (x)} [ \log(1-D ^ * (x)) ]$$
$$ \qquad \qquad \qquad \qquad = E_ {x \sim p_ {data} (x)} [ \frac{p_ {data} (x)}{p_ {data} (x) + p_ {g} (x)} ] + E_ {x \sim p_ {g} (x)} [ \frac{p_ {g} (x)}{p_ {data} (x) + p_ {g} (x)} ] $$
$$ \qquad \qquad \qquad \qquad \quad = - \log(4) + E_ {x \sim p_ {data} (x)} [ \log(p_ {data} (x)) - \log(\frac{p_ {data} (x) + p_ {g} (x)}{2}) ]$$
$$ \qquad \qquad + E_ {x \sim p_ {g} (x)} [ \log(p_ {g} (x)) - \log(\frac{p_ {data} (x) + p_ {g} (x)}{2}) ]$$
$$ \qquad \qquad \qquad \quad = - \log(4) + \text{KL} (p_ {data} || \frac{p_ {data} + p_ {g}}{2}) + \text{KL} (p_ {g} || \frac{p_ {data} + p_ {g}}{2}) $$
$$ = - \log(4) + 2 \times \text{JSD}(p_ {data} || p_ {g}) \qquad \qquad$$
결국, $D$가 최적화되어있는 상황에서 $G$를 최적화시키는 일은 $\text{JSD}(p_ {data} || p_ {g})$를 최소화 시키는 일과 같으며, 이 것은 결국 $p_ {data}$ 와 $p_ {g}$ 사이의 Jensen-Shannon Divergence를 최소화시키는 일로, Generated data의 distribution이 Real data의 distribution에 가까워지도록 하는 일이라는 뜻이 된다. GAN은 실제 주어진 data와 동일한 형태의 distribution을 구해나가는 알고리즘이며, 우리는 이로써 GAN이 주어진 dataset의 distribution을 알아내는 알고리즘이라는 결론을 얻을 수 있다.