Bayes Rule을 이용한 방식의 가장 큰 단점들 중 하나는 Likelihood의 Probability Distribution을 알아야 한다는 점입니다. 물론 앞선 포스팅에서는 관찰을 통해 Likelihood를 얻었지만, 여간 귀찮은 일이 아닐 뿐더러 완벽한 Distribution Function을 얻을 수 있는 것도 아닙니다. 그래서 우리는 Data로부터 직접 decision policy를 얻고자 합니다. 정해지지 않은 몇 개의 parameter로 이루어진 함수로 모델링을 한 후에, 이 모델이 주어진 Data를 가장 잘 설명하도록 parameter들을 구해낼 수 있다면 어떨까요? 사실 이러한 방식을 이용하는 대표적인 알고리즘이 바로 Deep Learning 입니다. 그리고 이 Deep Learning의 기본적인 Loss Function들은 대부분 Maximum Likelihood Estimation(MLE)과 Maximum A Posterior(MAP)를 통해 증명됩니다. 또한 확률을 기반으로 하기 때문에 이 두 이론을 공부하고 나면 확률과 Deep Learning 사이의 연결고리를 파악하는 데 큰 도움이 될 것입니다. 그러면 MLE와 MAP에 관해 본격적으로 알아보도록 합시다.
- 이 포스트가 속한 시리즈: Bayesian Deep Learning
- 선수 지식: 이 포스트를 이해하기 위해서는 Bayes’ Rule에 관한 지식이 필요합니다.
문제의 정의
Regression 문제를 생각하자. regression은 continuous한 input $x$를 넣었을 때 나오는 output $y$가 실제 정답 $t$와 같도록 만드는 문제이다. 즉 실제 output이 어떻게 될 지 예측하는 모델이다. 예를 들면 키를 보고 몸무게를 예측하는 모델이라고 하자. 이 모델을 학습시키기 위해 우리는 $N$명의 사람들에 대하여 실제 키($x_i$)와 동일 인물의 실제 몸무게($t_i$)를 조사한 결과인 Dataset $D$를 가지고 있다.
$$D = \{ (x_ 1, t_ 1), (x_ 2, t_ 2), (x_ 3, t_ 3), \cdots , (x_ N, t_ N) \}$$
이제 우리는 parameter $w$를 갖고 키($x$)를 넣으면 예측된 몸무게($y$)가 나오는 함수 $y(x|w)$를 정의하여, 가능한 모든 키($x$)에 대하여 예측된 몸무게($y(x|w)$)가 실제 몸무게($t$)에 최대한 가깝게 나오도록 $w$를 정해줘야 한다. 여기서 $w$는 $y(x|w)$가 갖는 parameter로, 일차함수($y=ax+b$)의 예를 들면 $a$와 $b$와 같은 계수를 의미한다. parameter는 하나의 값일 수도 있고 여러 개의 값일 수도 있으며, 벡터일 수도 있고 행렬일 수도 있다. 그냥 이러한 역할을 하는 parameter를 싸잡아서 $w$로 표현한 것이다. 이렇게 parameter들을 잘 학습하여 완벽한 모델 $y(x|w)$를 얻고 나면 우리는 모든 가능한 키($x$)에 대하여 실제 몸무게($t$)를 알고 싶다면 다음 식을 이용하면 된다고 말할 수 있다.
$$t = y(x|w)$$
그렇다면 우리는 항상 $t = y(x|w)$라고 말할 수 있을까? 아니다. 예측을 할 때는 겸손해야 한다. 즉 “실제 몸무게($t$)는 내가 예측한 몸무게($y$)과 정확히 일치한다!”라는 말은 실로 건방진 말이 아닐 수 없다. “실제 몸무게($t$)는 내가 예측한 몸무게($y$)일 확률이 가장 높지만, 아닐 수도 있어!”정도는 해 줘야 현명한 대답이 될 것이다. 여기서 “아닐 수도 있다!”의 의미는 우리의 예측 실력이 부족하기 때문이 아니다. 바로 데이터의 형태 때문이다. 예를 들어 보자. 키가 175cm인 사람 중에는 몸무게가 70kg인 사람도 있지만, 몸무게가 69kg인 사람도, 71kg인 사람도 충분히 존재한다. 우리는 애초에 $x=175$라는 input에 대해서 실제 몸무게($t$)를 100% 완벽하게 예측할 수 없다. 즉 우리가 예측하는 능력이 부족해서가 아니라, 근본적으로 발생하는 불확실성이라고 볼 수 있다.
그러면 이 말을 조금 더 수학적인 표현을 섞어 하면 어떻게 될까? “실제 몸무게는($t$)는 우리가 모르기 때문에 Random Variable인데, 그림1과 같이 내가 예측한 몸무게($y$)를 평균으로 하는 Gaussian 분포를 따른다고 볼 수 있다!”이렇게 말하면 앞에서 한 말과 비슷한 의미를 전달할 수 있게 된다. Gaussian 분포는 평균에서 확률 밀도가 가장 높기 때문이다.
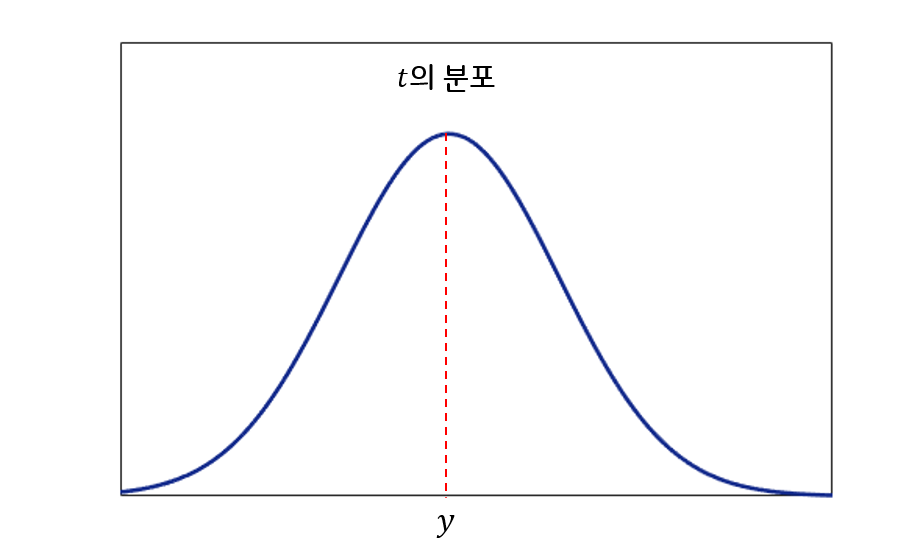
이를 조금 더 수학적인 표현을 이용해서 말하면 “실제 몸무게($t$)는 내가 예측한 몸무게($y$)를 평균으로 하고 특정 값 $\sigma$를 표준편차로 하는 Gaussian Distribution을 따른다”고 할 수 있고, 다음과 같이 쓸 수 있다.
$$t \sim N(y(x|w),\sigma^2) $$
$$p(t|x,w,\sigma) = \frac {1} {\sqrt{2\pi}\sigma} e^{-\frac{(t-y(x|w))^2}{2\sigma^2}}$$
여기서 $\sigma$는 무엇을 의미할까? 우리가 Gaussian Distribution을 이용하는 이유는 자신이 한 예측을 100% 확신할 수 없기 때문이라고 했다. 그래서 그림1과 같은 형태로 대답하게 된 것인데, 그림1에서 Distribution의 폭이 작다는 것($\sigma$가 작다는 것)은 무엇을 의미할까? 바로 우리가 예측한 값에 더 확신한다는 뜻이다. 반대로 폭이 크다는 것($\sigma$가 크다는 것)은 그 만큼 우리가 예측한 값에 자신이 없다는 뜻이다. 즉 $\sigma$는 우리가 한 예측이 얼마나 불확실한지의 정도를 나타낸다. 하지만 앞에서도 말했듯이 $\sigma$는 우리의 예측 능력에 따른 변수가 아니다. 우리가 풀려는 문제의 특성에 따라 설정되는 값이다. 우리가 풀려는 문제가 각 $x$에 대해서 $t$값이 대부분 하나로 일정하게 나오는 문제라면 $\sigma$는 작을 것이고, 위에서 설명한 몸무게 예측 문제처럼 $x$가 같더라도 다양한 $t$가 나올 수 있는 문제라면 $\sigma$는 클 것이다. 즉 우리가 문제의 특성을 파악하고 설정해주는 상수 값이다. 참고로 여기서는 이렇게 우리가 임의로 정해주게 되지만, 이후 포스팅에서는 중요하게 작용할 때가 오니 잘 기억해 두도록 하자.
Maximum Likelihood Estimation
위에서 유도했던 식을 다시 한 번 살펴보자.
$$p(t|x) = \frac {1} {\sqrt{2\pi}\sigma} e^{-\frac{(t-y(x|w))^2}{2\sigma^2}}$$
$\sigma$와 $w$는 parameter이므로 좌변의 notation에서 생략하였다. 여기서 $p(t|x)$가 의미하는 바는 무엇인가? 바로 input인 키가 $x$일 때 실제 몸무게가 $t$일 확률(밀도)이다. 변수가 continuous하기 때문에 확률 밀도라고 부르는 것이므로 편의상 확률이라고 하자. 이제 앞에서 학습을 위해 가지고 있던 Dataset을 다시 보도록 하자.
$$D = \{ (x_ 1, t_ 1), (x_ 2, t_ 2), (x_ 3, t_ 3), \cdots , (x_ N, t_ N) \}$$
$p(t|x)$의 의미는 키가 $x$일 때 실제 몸무게가 $t$일 확률이라고 하였는데, 그렇다면 Dataset이 위와 같이 구성될 확률($p(D)$)은 어떻게 구하면 될까? Dataset이 위와 같이 구성될 확률은 다시 말하면 “키가 $x_1$일 때 실제 몸무게가 $t_1$이고, 키가 $x_2$일 때 실제 몸무게가 $t_2$이고, $\cdots$, 키가 $x_N$일 때 실제 몸무게가 $t_N$일 확률”을 구하고 싶은 것인데, 각 data가 독립이라고 하였을 때, 곱의 법칙을 통해 다음과 같이 구할 수 있게 된다.
$$p(D) = \prod_ {i=1} ^ {N} {p(t_ i|x_ i)} = \prod_ {i=1} ^ {N} {\frac {1} {\sqrt{2\pi}\sigma} e^{-\frac{(t_ i-y(x_ i|w))^2}{2\sigma^2}}} $$
사실 그런데 이러한 $p(D)$ 값은 $w$에 따라 다르게 구해진다. 즉 “키가 $x_1$일 때 실제 몸무게가 $t_1$이고, 키가 $x_2$일 때 실제 몸무게가 $t_2$이고, $\cdots$, 키가 $x_N$일 때 실제 몸무게가 $t_N$일 확률”은 $w$에 따라 바뀔 수 있다. 그래서 $p(D)$ 보다는 $p(D|w)$라고 하자. 자, 그럼 이 상황에서 어떤 $w$를 구해야 가장 잘 예측하는 모델이 될까? 몸무게를 가장 잘 예측하는 모델은 다음과 같아야 할 것이다.
“키가 $x_1$일 때에는 실제 몸무게가 $t_1$일 확률이 가장 높다고 말하고, 키가 $x_2$일 때에는 실제 몸무게가 $t_2$일 확률이 가장 높다고 말하고, $\cdots$, 키가 $x_N$일 때에는 실제 몸무게가 $t_N$일 확률이 가장 높다고 말하는 모델”
다시 말하면 $p(D|w)$가 가장 높다고 대답하는 모델, 즉 $p(D|w)$가 최대가 되는 모델이어야 한다. 결국 우리가 해야 할 일은 $p(D|w)$가 최대가 되는 $w$를 찾는 것이고, 여기서 $p(D|w)$가 바로 likelihood기 때문에 이 방식의 이름이 Maximum Likelihood Estimation이다. $p(D|w)$을 왜 likelihood라고 부르는지는 뒤에서 설명하도록 하겠다.
Prior, Likelihood, Posterior
Prior, Likelihood, Posterior는 이전 포스트에서 분명히 다뤘던 내용이다. 이번 포스트에서는 농어와 연어를 벗어나서 Prior, Likelihood, Posterior의 일반적인 의미에 대해 짚고 넘어가려고 한다. 먼저 Prior, Likelihood, Posterior를 구분하기 위해서는 우리가 확률 또는 확률분포를 구하고자 하는 대상을 선택해야 한다. 이전 포스트에서는 그 대상이 농어($w_1$)인지 연어($w_2$)인지의 여부였다. 이 포스트에서, 그리고 일반적인 MLE, MAP를 포함하여 Deep Learning까지 대부분의 Machine Learning 알고리즘들이 구하고자 하는 대상은 바로 모델의 parameter인 $w$이다.
구하고자 하는 대상 다음으로 중요한 것이 바로 주어진 대상이다. 이전 포스트에서는 농어와 연어의 피부 밝기($x$)에 대한 정보가 주어졌다. 이번 포스트에서, 그리고 역시나 대부분의 Machine Learning 알고리즘들에게 주어진 대상은 당연히 Dataset, 즉 $D$가 된다. 이 두 개념을 이용하여 Prior, Likelihood, Posterior의 일반적인 의미를 파악해 보면 다음과 같다.
- Posterior: 주어진 대상이 주어졌을 경우, 구하고자 하는 대상의 확률 분포. 이 포스트에서는 $p(w|D)$.
- Likelihood: 구하고자 하는 대상을 모르지만 안다고 가정했을 경우, 주어진 대상의 분포. 이 포스트에서는 $p(D|w)$. $w$를 모르기 때문에 $w$에 대한 함수 형태로 나올 것이다.
- Prior: 주어진 대상들과 무관하게, 상식을 통해 우리가 구하고자 하는 대상에 대해 이미 알고 있는 사전 정보. 연구자의 경험을 통해 정해주어야 한다. 이 포스트에서는 $p(w)$.
이 사실들을 통해 Maximum Likelihood Estimation과 Maximum A Posterior의 이름의 뜻을 파악해볼 수 있을 것이다.
MLE의 계산
이제 다시 Maximum Likelihood Estimation으로 돌아가서 수식 전개를 해보도록 하자. Maximum Likelihood Estimation에서 우리가 해야 할 일은 바로 다음 식을 최대로 하는 $w$를 찾는 일이었다.
$$\mbox{likelihood} = p(D|w) = \prod_ {i=1} ^ {N} {p(t_ i|x_ i)} = \prod_ {i=1} ^ {N} {\frac {1} {\sqrt{2\pi}\sigma} e^{-\frac{(t_ i-y(x_ i|w))^2}{2\sigma^2}}} $$
이런 문제에서 우리는 주로 $\log$를 취해 준다. 많은 이유가 있지만 대표적으로는 두 가지 이유 때문이다. 먼저 likelihood가 최대면 likelihood의 $\log$ 값도 최대기 때문에 $\log$를 취해줘도 문제가 발생하지 않고, 또한 복잡한 곱셈 연산을 덧셈 연산으로 바꿔주기 때문에 수식의 전개가 용이하다.
$$\mbox{log likelihood} = \log{(p(D|w))} = \sum_ {i=1} ^ {N} \{ {-\log{(\sqrt{2\pi}\sigma)}-\frac{(t_ i-y(x_ i|w))^2}{2\sigma^2}} \}$$
이제 이 log likelihood를 최대가 되게 하는 $w$를 찾아주면 되는데, 알다시피 위 식의 $\sigma$와 $\pi$는 상수 값이다. 그렇기 때문에 log likelihood를 최대화시키는 $w$에 영향을 주지 않는다. 그래서 관련된 term들을 전부 제거한 다음, 앞의 부호를 바꿔주어 maximize 대신 minimize하기로 하면 다음 식이 남게 된다.
$$\sum_ {i=1} ^ {N} (t_ i-y(x_ i|w))^2$$
예측값과 실제 값의 차이의 제곱. L2 Loss이다. 일반적으로 Deep Learning에서 Regression 시에 가장 많이 쓰는 Loss 함수가 튀어나왔다. 이렇게 MLE를 이용하면 Regression에서 L2 Loss를 쓰는 이유를 증명해 낼 수 있다. 반대로, 우리가 앞으로 Deep Learning 등에서 L2 Loss를 이용한다는 것은 주어진 Data로부터 얻은 Likelihood를 최대화시키겠다는 뜻으로 해석할 수 있다. L2 Loss를 최소화 시키는 일은 Likelihood를 최대화 시키는 일인 것이다. 참고로 Classification 문제에서는 Bernoulli Distribution을 이용하면 비슷한 방법으로 Cross Entropy Error를 유도할 수 있다. 이에 관한 유도는 포스팅이 길어질 것이 우려되어, 궁금하신 분들은 이 포스트를 참고하시길 추천드린다.
Maximum A Posterior
Maximum Likelihood Estimation이 Likelihood를 최대화 시키는 작업이었다면, Maximum A Posterior는 이름 그대로 Posterior를 최대화 시키는 작업이다. Likelihood와 Posterior의 차이는 이전 포스트에서 다뤘듯이, Prior의 유무이다. Posterior는 Likelihood와 다르게 우리의 사전 지식인 Prior가 포함되어 있다. 즉 구하고자 하는 대상을 철저히 데이터만을 이용해서 구하고 싶다면 MLE를 이용하는 것이고, 데이터와 더불어 우리가 갖고 있는 사전 지식까지 반영하고 싶다면 MAP를 이용하는 것이다.
그렇다면 Prior를 반영해서 좋은 점은 무엇일까? 물론 우리가 매우 강력한 사전 지식을 갖고 있다면 $w$값을 구하는 데 있어서 매우 큰 도움이 될 것이다. 하지만 우리에게 별다른 사전 지식이 없더라도 Prior를 반영하는 것은 좋은 경우가 많다. output을 우리가 원하는 대로 제어할 수 있기 때문이다. 예를 들어 우리가 모델링한 함수 $y(x|w)$가 키($x$)를 줬을 때 몸무게($t$)를 잘 맞추게만 하고 싶으면 MLE를 써도 상관 없지만 잘 맞춤과 동시에 $y(x|w)$의 parameter $w$의 절댓값이 작기를 원한다면, 즉 0 주변에 분포해 있기를 원한다면 $w$가 0 주변에 분포한다는 Prior를 넣어 주어야 한다. 이렇게 output에 대한 특정 제약조건을 걸고 싶은 경우에 MAP를 쓰는 것이 좋다.
Posterior를 Maximize해야 하는 이유는 Likelihood의 경우보다 단순하다. Posterior는 애초에 $w$의 확률 분포기 때문에 $w$가 될 확률이 가장 높은 값으로 정해주는 것이다. 그렇다면 본격적으로 Posterior를 구해서 Maximize 해보도록 하자. 이전 포스트에 따르면 Posterior는 다음과 같이 구할 수 있다.
$$P(w|D) = \frac {P(D|w)P(w)}{\int {P(D|w)P(w)} dw}$$
분모가 integral 식으로 바뀐 이유는 $w$가 continuous하기 때문이다. 하지만 겁먹을 것 없는 게, $w$에 대해서는 적분을 하고 있고, $D$는 주어진 값이기 때문에 결국 $\int {P(D|w)P(w)} dw$는 상수가 되어 $\eta$로 치환 가능하다. 기왕 치환하는거 $\eta = \frac{1}{\int {P(D|w)P(w)} dw}$로 치환하자.
$$P(w|D) = \eta P(D|w)P(w)$$
그러면 이제 $w$의 Prior를 정해주어야 하는데, 위에서 말했던 것 처럼, $w$에 대한 특별한 사전 지식은 갖고 있지 않은 상황이다. 그러므로 우리 나름대로의 제약조건을 걸어주도록 하자. Deep Learning에서 Overfitting을 방지하기 위해 사용하는 방법들 중에 Weight Decay(Regularization)라는 방식이 있다. Loss에 $w^2$ 또는 $|w|$ 등을 추가하여 $w$ 자체의 크기를 줄여 네트워크의 표현력을 감소시키는 방식인데, 이 방식을 우리는 MAP를 이용해 유도할 것이다. 우리의 목표는 다음과 같다.
“Overfitting을 방지하기 위해서는 네트워크의 표현력을 감소시켜야 하는데, 그러기 위해서는 $w$의 절댓값이 작아야 한다. 즉 0 주변에 분포하여야 한다.”
$w$의 크기를 줄이는 방식에는 여러 가지가 있겠지만, 우리는 $w$에 Prior를 걸어 줄 것이다. $w$에 0을 평균으로 하는 Gaussian Distribution이라는 Prior를 걸어주게 되면, $w$는 자연스럽게 0 주변에 배치 될 것이다.
$$w \sim N(0,\sigma_w ^2) $$
$$p(w) = \frac {1} {\sqrt{2\pi}\sigma _ w} e^{-\frac{w^2}{2\sigma _ w ^2}}$$
먼저 likelihood에서와 같이 Posterior에 $\log$를 취해주도록 하자. 그리고 그 값을 최대로 하는 $w$를 찾는 것이 우리의 목표이다.
$$w^* = \mbox{argmax}_w \{ \log p(w|D) \}$$
$$\qquad \qquad \qquad \qquad \quad = \mbox{argmax}_w \{ \log \eta + \log p(D|w) + \log p(w) \}$$
여기서 $\log p(D|w)$는 Likelihood 이므로 이 값을 Maximize하는 것은 위에서 봤듯이 $\sum_ {i=1} ^ {N} (t_ i-y(x_ i|w))^2$를 Minimize 하는 것과 같다. 길기 때문에 $L(w) = \sum_ {i=1} ^ {N} (t_ i-y(x_ i|w))^2$라고 치환하여 대입하면 다음과 같다.
$$w^* = \mbox{argmax}_w \{ \log \eta - L(w) + \log p(w) \}$$
이제 $\log p(w)$ 식을 대입하면 다음과 같게 된다.
$$w^* = \mbox{argmax}_w \{ \log \eta - L(w) -\log{(\sqrt{2\pi}\sigma _ w)} -\frac{w^2}{2 \sigma _ w ^ 2} \}$$
여기서 $\eta$, $\pi$, $\sigma _ w$는 전부 상수이므로 관련된 term들을 제거해주면 다음 식을 Minimize하는 문제가 된다.
$$L(w) + \frac{w^2}{2 \sigma _ w ^ 2} = \sum_ {i=1} ^ {N} (t_ i-y(x_ i|w))^2 + \frac{w^2}{2 \sigma _ w ^ 2}$$
$\frac{1}{2 \sigma _ w ^ 2}$는 상수이므로 $\alpha$ 등으로 치환하면 Weight Decay(L2 Regularization) 방식을 적용한 Deep Learning의 Loss 함수가 된다. 우리는 Gaussian Distribution을 Prior로 준 문제의 MAP로부터 Weight Decay 식을 유도해 낸 것이다. 또한 우리가 앞으로 Deep Learning 등에서 Weight Decay, 그 중에서도 L2 Regularization을 쓴다는 것은 주어진 Data를 적용함과 동시에 $w$에 Gaussian Distribution이라는 Prior를 걸어 주어 MAP를 통해 $w$를 구하겠다는 것으로 해석할 수 있다. L2 Regularization을 적용하는 일은 $w$에 Gaussian Distribution을 Prior로 걸어 주는 일인 것이다. 참고로 Laplacian Distribution을 Prior로 걸어 주면 L1 Regularization을 얻을 수 있다. 직접 해보기 어렵지 않을 것이다.