기계학습에서는 특정 dataset의 분포를 추정하기 위해 그 집단을 대표하는 Sample을 뽑아 관찰하는 기법을 사용합니다. 예를 들어 참치와 고등어가 서식하는 바다에서 10마리의 물고기를 잡았을 때 참치 1마리와 9마리의 고등어가 잡혔다면, 우리는 이 바다에 살고 있는 물고기가 대략 참치 10%와 고등어 90%로 이루어져 있다고 짐작할 수 있습니다.
그렇다면 우리가 데이터의 분포를 추정했을 때 얼마나 잘 추정한 것인지 측정하는 방법은 없을까요? 오늘 소개해 드릴 Kullback-Leibler Divergence 와 Jensen-Shannon Divergence는 서로 다른 확률 분포의 차이를 즉정하는 척도입니다. 우리가 추정한 확률 분포와 실제 확률 분포 사이의 차이가 작다면 좋은 추정이라고 할 수 있습니다.
또한 기계학습에서는 복잡한 함수나 분포를 단순화 하여 하나의 간단한 함수로 나타내려는 노력을 많이 합니다. 예를 들어 실제 측정 결과 얻은 복잡한 확률 분포를 비교적 적은 파라미터를 갖는 Gaussian Distribution 등으로 근사한다면 약간의 오차는 있겠지만 정보를 저장하는 데 드는 비용을 크게 절감할 수 있을 것입니다. 이 때도 역시 가장 오차가 적은 Model로 근사하기 위해 위와 같은 척도들을 이용합니다. 이번 포스팅에서는 두 확률 분포 간의 차이를 나타내는 척도인 Kullback-Leibler Divergence 와 Jensen-Shannon Divergence에 대하여 알아보도록 하겠습니다.
- 선수 지식: 이 포스트를 이해하기 위해서는 Entropy & Information Theory에 관한 이해가 필요합니다.
- 이 자료의 도움을 많이 받았습니다: COUNT BAYESIE Blog
알파벳 맞추기 게임
앞의 Entropy & Information Theory 포스트에서 알파벳 맞추기 게임에 관한 예를 들었었다. 알파벳 맞추기 게임의 규칙에 관한 내용은 이 포스트에서 필요 없으니 선수 지식이 있다면 굳이 읽어 볼 필요는 없다. 우리는 위의 5종류의 알파벳이 쓰인 카드들 중에서 하나를 골라야 하는데, 각 알파벳이 뽑힐 확률은 다음과 같다고 하자.
| 카드에 쓰인 알파벳($s_ {i}$) | a | b | c | d | e |
|---|---|---|---|---|---|
| 그 카드를 뽑을 확률($p_ {i} = P(s_ {i})$) | 1⁄9 | 2⁄9 | 1⁄3 | 2⁄9 | 1⁄9 |
이 확률 분포를 그래프로 나타내면 다음과 같다.
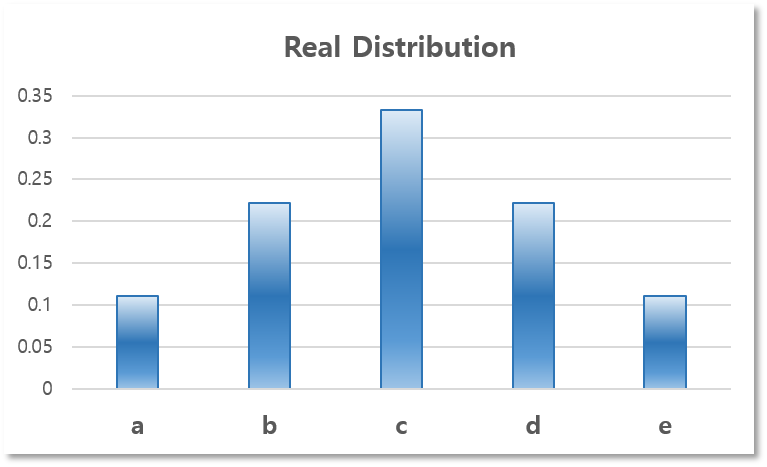
하지만 이와 같이 표로 나타내는 것은 정보를 저장하는데 많은 용량이 필요하며 수학적으로 다루기가 까다롭다. 그렇기 때문에 우리는 위 확률 분포를 많이 쓰이는 확률 분포 모델로 근사하기로 하자.
확률 분포 근사
먼저, 복잡하게 생각하기 귀찮으니 모든 알파벳이 뽑힐 확률을 근사적으로 같다고 생각해 버리도록 하자.
$$P_ {i} = \frac{1}{5}, i \in \{ 0,1,2,3,4 \}$$
즉, Uniform Distribution으로 근사한 것이며, 다음과 같은 확률 분포를 갖게 될 것이다.
| 카드에 쓰인 알파벳($s_i$) | a | b | c | d | e |
|---|---|---|---|---|---|
| 그 카드를 뽑을 확률($p_i = P(s_i)$) | 1⁄5 | 1⁄5 | 1⁄5 | 1⁄5 | 1⁄5 |
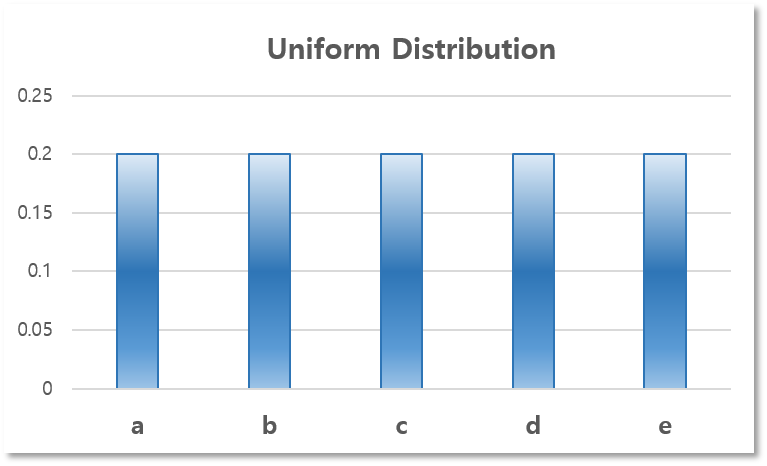
모두 같게 근사를 했더니, 스스로 생각해 봐도 너무 대충 근사한 느낌이 든다. 그래서 두 번째 안으로는 다음과 같이 Binomial Distribution을 이용하여 근사해 보도록 하자. $$P_i = {4 \choose i}(\frac{1}{2})^i(\frac{1}{2})^{4-i}, i \in \{ 0,1,2,3,4 \}$$
| 카드에 쓰인 알파벳($s_i$) | a | b | c | d | e |
|---|---|---|---|---|---|
| 그 카드를 뽑을 확률($p_i = P(s_i)$) | 1⁄16 | 1⁄4 | 3⁄8 | 1⁄4 | 1⁄16 |
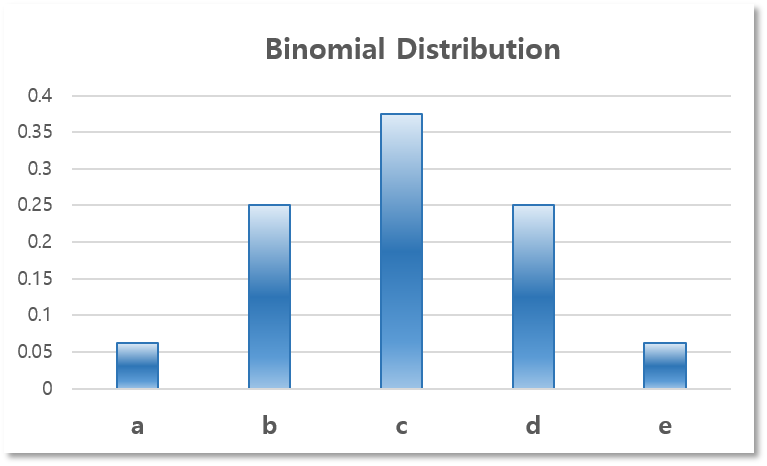
우리에게는 카드가 나올 확률을 표현할만한 두 가지 모델이 존재한다. 그렇다면 어떤 모델이 실제 확률 분포를 더 잘 표현할까? 즉, 어떤 모델이 실제 확률 분포와 더 닮았을까? 우리는 해당 모델이 실제 모델과 얼마나 닮았는지 알기 위한 정량적인 척도가 필요하다. 이러한 척도중 하나가 바로 Kullback-Leibler Divergence(KL-Divergence)이다. 다음 장에서 더 자세히 알아보도록 하자.
Kullback-Leibler Divergence
Kullback-Leibler Divergence는 앞에서 살펴봤듯이 두 모델이 얼마나 비슷하게 생겼는지를 알기 위한 척도인데, 제시한 모델이 실제 모델의 각 item들의 정보량을 얼마나 잘 보존하는지를 측정한다. 즉, 원본 데이터가 가지고 있는 정보량을 잘 보존할 수록 원본 데이터와 비슷한 모델이라는 것이다. 먼저 item $s_i$가 갖는 정보량은 다음과 같이 계산하였다.
$$I_i = -\log(p_i)$$
그리고 원본 확률 분포 $p$ 와 근사된 분포 $q$에 대하여 i번째 item이 가진 정보량의 차이(정보 손실량)는 다음과 같을 것이다.
$$\Delta I_i = \log(p_i) - \log(q_i)$$
$p$에 대하여 이러한 정보 손실량의 기댓값을 구한 것이 바로 KL-Divergence이다.
$$D_{KL} (p||q)= E[\log(p_i) - \log(q_i)] = \sum_i {p_i \log \frac{p_i}{q_i}}$$
간단히 말하면, KL-Divergence는 근사시 발생하는 정보 손실량의 기댓값이다. 이 값이 작을 수록 더 가깝게 근사한 것이라고 할 수 있다. 그러면 이제 위 두 모델중에 어떤 모델이 원본과 더 가까운지 측정해보도록 하자.
| Model | KL-Divergence |
|---|---|
| Uniform Distribution | $\frac{1}{9}\log(\frac{5}{9}) + \frac{2}{9}\log(\frac{10}{9}) + \frac{1}{3}\log(\frac{5}{3}) + \frac{2}{9}\log(\frac{10}{9}) + \frac{1}{9}\log(\frac{5}{9}) = 0.0865$ |
| Binomial Distribution | $\frac{1}{9}\log(\frac{16}{9}) + \frac{2}{9}\log(\frac{8}{9}) + \frac{1}{3}\log(\frac{8}{9}) + \frac{2}{9}\log(\frac{8}{9}) + \frac{1}{9}\log(\frac{16}{9}) = 0.0362$ |
계산 결과, Binomial Distribution으로 근사하는 것이 더 효과적이라는 결론을 얻을 수 있다.
Jensen-Shannon Divergence
당연하게도, KL-Divergence는 근사된 확률 분포가 얼마나 원본과 비슷한지를 측정하는 척도 이외에도, 단순히 두 대등한 확률 분포가 얼마나 닮았는지를 측정하는 척도로 쓰일 수 있다. 하지만 포스트를 읽으면서 눈치 채신 분들도 있겠지만, KL-Divergence는 Symmetric하지 않다. 즉 $D_ {KL} (p||q) \neq D_ {KL} (q||p)$이다. 그렇기 때문에 KL-Divergence를 Symmetric하게끔 개량한 Jensen-Shannon Divergence를 쓴다.
$$\text{JSD}(p,q) = \frac{1}{2}D_ {KL} (p||\frac{p+q}{2}) + \frac{1}{2}D_ {KL} (q||\frac{p+q}{2})$$
그러면 $\text{JSD}(p,q) = \text{JSD}(q,p)$가 되어, 두 확률 분포 사이의 distance로서의 역할을 할 수 있게 된다.