안녕하세요. 오늘은 Quanzeng You의 CVPR 논문인 [Image Captioning with Semantic Attention]에 대한 리뷰를 하려고 합니다. Image Captioning은 인공지능 학계의 거대한 두 흐름인 ‘Computer Vision(컴퓨터 비전)’과 ‘Natural Language Processing(자연어 처리)’를 연결하는, 매우 중요한 의의를 갖는 연구 분야입니다. 이번 논문을 통해 제 주 관심 분야인 Video Understanding의 가장 기초라고 할 수 있는 Image Captioning 알고리즘이 어떠한 방식으로 구현되는지 알아보도록 하겠습니다.
Introduction
1. Top-Down & Bottom-Up Approach
이 논문은 ‘Sementic Attention’을 이용한 ‘Image Captioning’ 알고리즘을 제안하는 논문이다.
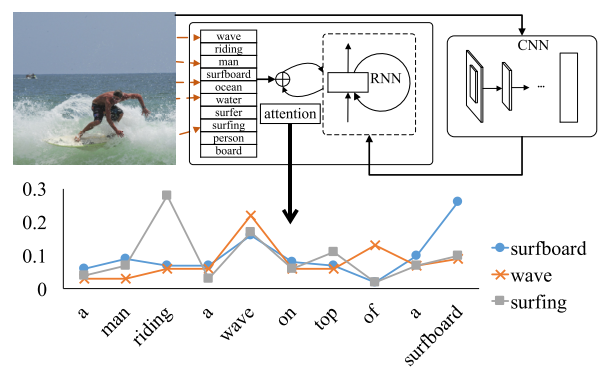
Image Captioning은 말 그대로 이미지의 캡션을 달아주는 일, 즉 이미지를 보고 어떤 이미지인지 언어로 설명하는 작업이다. 그림 1은 서핑을 하고 있는 한 남자의 이미지에 대한 캡션을 생성한 결과를 보여주고 있다. 컴퓨터는 해당 이미지에 대하여 ‘A man riding a wave on top of a surfboard’라는 캡션을 도출하였으며 이는 이미지를 매우 잘 설명하고 있음을 알 수 있다. 어찌 보면 정말 신기한 일이 아닐 수 없는데, 논문을 읽어 가며 이 일이 어떻게 하여 가능하게 되었는지를 알아보도록 할 것이다.
Image Captioning의 접근 방식은 크게 ‘Top-Down Approach’와 ‘Bottom-Up Approach’로 구분된다. Top-Down Approach에서는 이미지를 통째로 시스템에 통과 시켜서 얻은 ‘요점’을 언어로 변환하는 반면 Bottom-Up Approach에서는 이미지의 다양한 부분들로부터 단어들을 도출해내고, 이를 결합하여 문장을 얻어낸다. 현재 가장 많이 쓰이고 있느 접근 방식은 Top-Down Approach인데, 그 이유는 Recurrent Neural Network(RNN)를 이용하여 각 Parameter들을 Train Data로부터 학습시킬 수 있으며, 이 방식의 성능이 가장 좋다고 평가받기 때문이다.
하지만, 이러한 Top-Down Approach의 단점은 이미지의 디테일한 부분들에 집중하는 것이 상대적으로 어렵다는 점이다. 반면 Bottom-Up Approach는 이미지의 모든 부분으로부터 하나씩 뽑아낸 단어들을 조합하기 때문에 디테일에까지 신경을 써줄 수 있다.
2. Visual Attention
논문에서는 앞에서 살펴본 Top-Down Approach와 Bottom-Up Approach의 장점을 합해서 Image Captioning 성능을 올리고자 한다. 이 때 사용되는 개념이 바로 Visual Attention이다.
Visual Attention은 말 그대로 이미지의 특정 부분에 집중하는 것이다. 사람이 이미지의 모든 내용을 전부 묘사하지 않는 것처럼, 컴퓨터도 이미지에서 특히 중요한 부분에 자원을 집중하는 형태의 노력이 필요하다. Visual Attention을 통해서 컴퓨터는 이미지의 특히 중요한 부분에 집중하고, 더 자세히 묘사하게 된다. Visual Attention이 알고리즘적으로 어떻게 적용되는지는 뒤에서 살펴보도록 하자.
Sementic attention for image captioning
1. Overall Framework
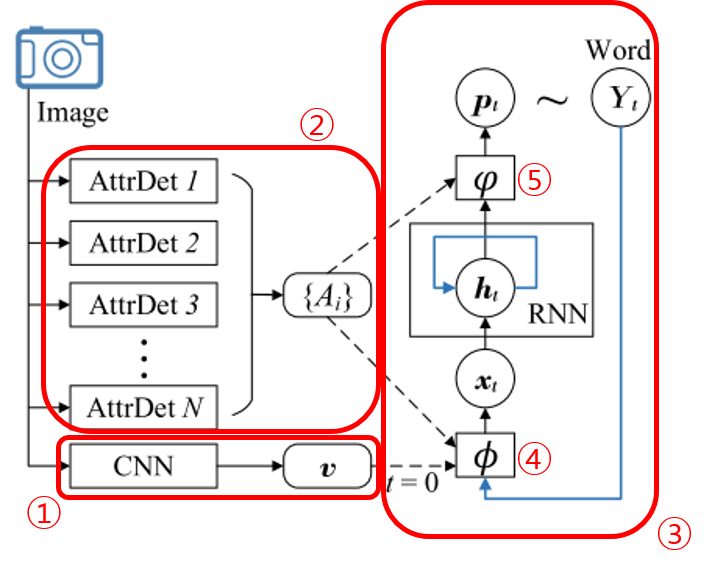
그림 2를 보도록 하자. 논문에서 제안하는 알고리즘은 이미지가 CNN을 통과하는 과정에서 생성된 Feature인 $v$를 얻으면서 시작된다(①). 사람이 이미지를 이해할 때에도 처음부터 대상의 세세한 부분을 먼저 보지 않는 것 처럼 알고리즘도 이미지의 전체적인 특징을 확인한 후에 구체적인 부분들을 관찰하게 되는데, 이 특징이 바로 $v$이다. 이 논문에서 $v$는 특별한 CNN이 아니라 Google Net과 같이 Classification을 목적으로 Pre-Trained 된 네트워크를 이용하여 뽑아 낸다.
②는 이미지로부터 Bottom-Up 방식을 통해 얻어진 특징들의 집합으로, $\{ A_ {i} \}$로 표현하며 Attribute라고 부른다. 즉 이미지에 등장하는 다양한 사물들이나 이벤트, 동작들을 Detector를 통해 검출해 낸 결과이다. 검출의 방식은 뒤에서 알아보도록 하자. 검출된 부분 이미지들은 각각 그에 해당하는 단어가 존재하게 된다. 예를 들어서 전체 영상으로부터 서핑보드에 해당하는 부분을 검출해 냈다면, 이 부분에 해당하는 단어는 ‘서핑보드’가 된다. 다시 말해서, 전체 이미지로부터 뽑은 부분적인 이미지들은 미리 준비된, 모든 단어들의 집합인 $\mathcal{Y}$(dictionary)의 한 원소와 대응된다.
③은 RNN(Recurrent Neural Network)으로, 문장의 각 단어를 순서대로 출력하게 된다(정확히 말하면, $t$번째 state에서 $t$번째 단어에 해당하는 Softmax 값인 $p_ {t} \in \mathbb{R}^ {|\mathcal{Y}|}$를 출력하고, 확률 값이 가장 큰 class를 찾아서 $Y_ {t} \in \mathcal{Y}$를 얻는다). 또한 RNN의 input은 ①과 ②를 통해 얻은 특징들과 $t-1$번째로 출력된 단어(바로 이전에 출력된 단어)가 된다.
먼저 $t=0$ 상태에서 $v$가 input으로 들어가게 된다. 그러면 RNN은 첫 번째 단어인 $Y_ {0}$를 출력하게 된다.
$t>0$에서는 더이상 $v$는 input으로 들어가지 않는다. 그 대신 $\{ A_ {i} \}$와, 바로 직전 state에서 출력되었던 단어인 $Y_ {t-1}$를 input으로 함께 받는다. 이미지의 각 부분에 대한 정보와 현재 본인이 어떤 말을 하던 중이었는지에 대한 정보다.
여기서 의문이 한 가지 생긴다. $\{ A_ {i} \}$는 모든 state에 대해 매 번 똑같이 입력되는 것인가? 그렇게 하는 것이 의미가 있는가? 정답부터 말하면 ‘아니다’ 이다. 정확히는 $\{ A_ {i} \}$가 매 state마다 RNN의 input으로 입력되는 것은 맞지만, 입력되는 방식이 계속 변화한다. ④를 보면 알 수 있다.
RNN의 input단에서는 $v$, $Y_ {t-1}$, $\{ A_ {i} \}$를 입력 신호로 받는데, 이 신호들이 곧바로 RNN의 입력($x_ {t}$)가 되는 것이 아니다. RNN의 input 단에 문지기처럼 붙어 있는 $\phi()$가 위 신호들을 RNN에 입력 가능한 형태인 $x_ {t}$로 바꿔 준다. 이 것을 input model이라고 부르며, 현재까지 본인이 한 말들($Y_ {t-1}$)을 이미지로부터의 정보($\{ A_ {i} \}$)와 관련짓고 이해하는 역할을 하는 부분이다. $t$에 따라서 $\phi()$가 변화하기 때문에, $\{ A_ {i} \}$가 매 state마다 RNN에 입력되는 방식은 $t$에 따라 변화하게 된다.
Input model과 더불어 output model(⑤) 또한 존재하는데, $\varphi()$로 표현한다. 이는 $\{ A_ {i} \}$와 RNN의 output인 $h_ {t}$를 받아서 다음에 올 단어를 예측하는 역할을 하게 된다. 예측의 결과는 각 단어별로 등장할 확률들의 벡터인 $p_ {t}$로 나오게 되고, $\mathcal{Y}$에서 확률이 가장 높은 원소를 다음 단어 $Y_ {t}$로 정하게 된다. $t=0$일 경우 $\phi()$는 단순한 Linear Model을 통해 $x_ {t}$와의 dimension만 맞춰주게된다. 다른 경우의 $\phi()$와 $\varphi()$의 내부 구조는 뒤에서 알아보도록 하자.
위의 설명들을 간단하게 식으로 나타내면 다음과 같이 표현할 수 있다.
$$x_ {0} = \phi_ {0} (v) = W^ {x,v}v$$
$$h_ {t} = RNN(h_ {t-1}, x_ {t})$$
$$Y_ {t} \sim p_ {t} = \varphi_ {t} (h_ {t}, \{ A_ {i} \}) $$
$$x_ {t} = \phi_ {t} (Y_ {t-1}, \{ A_ {i} \}), \space t>0 $$
$\phi()$와 $\varphi()$의 공통점은 둘 다 $\{ A_ {i} \}$를 입력받는다는 점이다. 또한 $t$에 따라 $\{ A_ {i} \}$가 입력되는 방식이 변한다고 하였는데, 구체적으로는 $\{ A_ {i} \}$에서 $i$에 따라 각 Attribute에 집중하는 정도를 $t$에 따라 달리 하는 것이다. 이 것이 바로 Attention Model이다. 그러므로 Attention Model은 $\{ A_ {i} \}$를 이용하는 input model과 output model에 전부 적용된다. 각각의 model에 적용되는 Attention Model을 각각 Input Attention Model과 Output Attention Model이라고 부르도록 하자.
2. Input Attention Model
Input Attention Model은 이미지의 각 부분으로부터 뽑아 낸 특징(Attribute)들의 집합인 $\{ A_ {i} \}$와 이전 state에서 출력된 단어인 $Y_ {t-1}$를 입력받는다. 먼저 이 두 input을 연산 가능한 vector의 형태로 바꿔야 하는데, 먼저 $Y_ {t-1}$는 모든 단어들의 집합인 $\mathcal{Y}$와의 비교를 통해 one-hot vector로 표현 가능하다. 그 벡터를 $y_ {t-1}$라 하자. 또한 앞에서도 말했듯이 $\{ A_ {i} \}$의 원소 $A_ {i}$에 대하여 이에 대응하는 $\mathcal{Y}$ 안의 단어를 찾을 수 있으며, 이에 해당하는 one-hot vector를 $y^ {i}$라 하자.(이제부터 각 state에 대한 index $t$는 아래첨자로, 각 Attribute에 대한 index $i$는 위첨자로 표현하도록 하겠다.)
이렇게 얻은 $y_ {t-1}$와 $y^ {i}$로부터 우리는 ‘state $t$에서 $i$번째 attribute에 가해지는 집중의 정도(attention)’을 정의할 수 있게 되며, 이 것을 $\alpha_ {t} ^ {i}$로 표현하도록 하자. $\alpha_ {t} ^ {i}$는 직접 학습되지 않고, 다음과 같이 $y_ {t-1}$와 $y^ {i}$를 input으로 하는 함수를 모델링 하여 Parameter인 $\tilde{U}$를 학습하게 된다. ($\tilde{U}$는 $i$, $t$와 무관한 값이다. 즉 모든 state의 모든 Attribute들은 전부 하나의 $\tilde{U}$를 공유하게 된다.)
$$\alpha_ {t} ^ {i} \propto \exp (y_ {t-1} ^ {T} \tilde{U} y^ {i}) $$
$y_ {t-1} ^ {T} \tilde{U} y^ {i}$은 $y_ {t-1}$와 $y^ {i}$로부터 성분을 하나씩 뽑아 곱한 항의 모든 가능한 조합들을 $\tilde{U} \in \mathbb{R}^ {|\mathcal{Y}| \times |\mathcal{Y}|}$의 성분을 parameter로 하여 Linear Combination한 것이며, exponential을 취해 준 이유는 $\alpha_ {t} ^ {i}$가 $\{ A_ {i} \}$의 각 항에 곱해지는 weight이기 때문에 Softmax처럼 확률화 시켜 준 것이다.
이 쯤 되면 지금까지 외면해왔지만, 꼭 한 번 짚고 넘어가야 할 문제점이 하나 있다. 바로 $|\mathcal{Y}|$의 크기이다. Captioning 알고리즘이 아무리 좋다 해도 $\mathcal{Y}$에 없는 단어는 사용할 수 없다. 그렇기 때문에 $\mathcal{Y}$에는, 세상에 존재하는 가능한 한 많은 단어들이 존재해야 한다. 그렇기 때문에 $|\mathcal{Y}|$의 값은 어마어마하게 커질 수 밖에 없으며, 이로 인해 one-hot vector들의 dimension 또한 커지고, $\tilde{U}$의 학습시켜야 하는 parameter 수는 상상을 초월하게 된다.
사실 one-hot vector는 각 vector들의 correlation이 전부 0이 되도록, 즉 모든 vector들이 서로 독립이 되도록 만들기 위해 dimension을 최대로 늘린 것이다. 하지만 실제 자연어의 세계에는 서로 연관되어 있는 단어들이 너무나도 많기 때문에 이러한 성질을 이용하여 각 단어를 나타내는 vector의 dimension도 줄이고, 비슷한 의미의 단어들끼리 근처에 위치하도록 조정하는 Word2Vec이나 Glove와 같은 알고리즘이 존재한다. 이 알고리즘들을 통해 one-hot vector들을 $d$-dimensional domain으로 embedding할 수 있는 행렬 $E \in \mathbb{R}^ {d \times |\mathcal{Y}|}$를 얻을 수 있고, 위 식은 다음과 같이 수정된다.
$$\alpha_ {t} ^ {i} \propto \exp ((Ey_ {t-1})^ {T} U Ey^ {i}) = \exp (y_ {t-1} ^ {T} E^ {T} U Ey^ {i}), \space \tilde{U} = E^ {T} U E$$
위 식에서 $U \in \mathbb{R}^ {d \times d}$만 학습시키면 되기 때문에 학습시켜야 할 parameter의 양이 크게 줄어들게 된다. 정확한 $\alpha_ {t} ^ {i}$ 값을 구하기 위해 Normalization 과정을 거치면 다음과 같이 될 것이다.
$$\alpha_ {t} ^ {i} = \frac{\exp (y_ {t-1} ^ {T} E^ {T} U Ey^ {i})}{\sum_ {j} \exp (y_ {t-1} ^ {T} E^ {T} U Ey^ {j})}$$
위 식을 통해 $\alpha_ {t} ^ {i}$를 구하면, 최종적으로 $x_ {t}$는 다음과 같이 구하게 된다.
$$x_ {t} = W^ {x, Y} (Ey_ {t-1} + \mbox{diag} (w^ {x,A}) \sum_ {i} \alpha_ {t} ^ {i} Ey^ {i}) $$
단순히 이미지의 각 Attribute에 대한 Attention 결과와 $t-1$에서 출력된 단어를 더하는 함수인데, $\sum_ {i} \alpha_ {t} ^ {i} Ey^ {i}$은 word vector domain이 아니므로 $Ey_ {t-1}$와 더해지기 위해서는 추가적인 조정이 필요하다. 그렇기 때문에 $\mbox{diag} (w^ {x,A})$를 곱해 domain을 맞춰준 것이며, 마찬가지로 $(Ey_ {t-1} + \mbox{diag} (w^ {x,A}) \sum_ {i} \alpha_ {t} ^ {i} Ey^ {i})$와 $x_ {t}$의 domain이 다르기 때문에 맞춰주기 위해서 $W^ {x, Y}$를 곱하게 된다.
3. Output Attention Model
$\phi()$와 $\varphi()$는 둘다 attention model을 이용하지만, 당연하게도, 서로 다른 attention weight를 이용한다. 위에서도 언급했듯이, 수행하는 역할이 서로 다른 Attention Model이기 때문이다. $\varphi()$는 $h_ {t}$와 Attribute $\{ A_ {i} \}$를 입력받게 되고, 각 $A_ {i}$에 대해 Input Attention Mdoel에서와 같이 대응되는 Word Vector $Ey^ {i}$가 존재한다. 이를 이용하여 Output attention weight $\beta_ {t} ^ {i}$는 다음과 같이 구할 수 있다.
$$\beta_ {t} ^ {i} \propto \exp (h_ {t} ^ {T} V \sigma (Ey^ {i}))$$
등식이 아닌 비례식인 이유는 $\beta_ {t} ^ {i}$도 $\alpha_ {t} ^ {i}$와 같이 Softmax Normalization을 해 줘야 하기 때문이며, $Ey^ {i}$가 sigmoid 함수($\sigma$)를 거치는 이유는 $h_ {t}$또한 sigmoid를 거친 값이기 때문이다. 이렇게 해서 attention weight를 얻으면, $\varphi()$는 다음 단어를 예측하는 Somftmax 확률 벡터를 출력한다. 이는 다음과 같이 계산된다.
$$p_ {t} \propto \exp(E^ {T} W^ {Y,h} (h_ {t} + \mbox{diag}(w^ {Y,A}) \sum_ {i} \beta_ {t} ^ {i} \sigma (Ey^ {i}))) $$
$\mbox{diag}(w^ {Y,A})$와 $W^ {Y,h}$이 곱해진 이유는 Input Attention Model에서와 동일하다. Input Attention Model과 다른 점을 살펴 보면, 가장 바깥 쪽에 곱해진 $E^ {T}$인데, 이 것은 현재 $W^ {Y,h} (h_ {t} + \mbox{diag}(w^ {Y,A}) \sum_ {i} \beta_ {t} ^ {i} \sigma (Ey^ {i}))$가 $d$-dimensional vector domain이므로 다시 one-hot vector들의 word domain으로 바꾸기 위해서 곱해준 것이다(vec2word). $\exp$가 붙은 이유와 등식이 아닌 비례식인 이유는 역시 Softmax Normalization을 해 줘야 하기 때문이다.
4. Model Learning
RNN Model을 학습시키기 위해 우리가 갖고 있는 데이터는 CNN으로 부터 얻은 전반적인 Feature $v$와 Detector로부터 얻은 Attribute $\{ A_ {i} \}$, 그리고 각 이미지에 대해 우리가 ground truth로 갖고 있는 캡션으로부터 얻은 단어들의 Sequence $Y_ {t}$가 있다. 또한 우리는 Attention Model의 parameter들인 $\Theta_ {A} = \{ U, V, W^ {*,*}, w^ {*,*} \}$와 RNN 내부의 parameter들($\Theta_ {R}$)을 학습시켜야 한다. $t$번째 단어의 ground truth $Y_ {t}$에 대하여 Model의 Softmax output vector에서 $Y_ {t}$에 해당하는 확률을 $p(Y_ {t})$라고 하면, 모든 $t$에 대하여 다음과 같은 Cross-Entropy Error를 계산할 수 있다.
$$Cross \space Entropy = - \sum_ {t} \log{p(Y_ {t})} $$
여기에 추가적으로, 특정 Attribute에 attention이 과도하게 집중되는 것을 막기 위하여 다음과 같은 Regulariztion Term을 추가한다.
$$g(\boldsymbol{\alpha}) = \lVert \boldsymbol{\alpha} \rVert _ {1,p} + \lVert \boldsymbol{\alpha^ {T}} \rVert _ {q,1} = [\sum_i [ \sum_t \alpha^i_t]^p]^{1/p} + \sum_t [\sum_i (\alpha^i_t)^q]^{1/q}, \space ( p > 1, \space 0 < q < 1 )$$
그러면 최종적으로 다음과 같은 식을 최적화 하면 되는 문제가 된다.
$$\min_ {\Theta_ {A}, \Theta_ {B}} -\sum_ {t} {\log{p(Y_ {t})}} + g(\boldsymbol{\alpha}) + g(\boldsymbol{\beta}) $$
Visual Attribute Prediction
자, 이제 한 가지의 일만 남았다. 이제까지 일단 모르는 상태로 넘어왔었던 Attribute를 얻어내는 방법에 대한 논의가 필요하다. 논문에서는 이 Attribute를 얻는 방법을 두 가지 설명하는데, 하나는 Parametric Method이고 다른 하나는 Non-parametric Method이다. 둘 다 어렵지 않으니 하나씩 살펴보도록 하자.
1. Non-parametric attribute prediction
Medeia의 발전으로 인해, 우리에게는 매우 방대한 양의 이미지 data들과, 이에 대한 caption들이 있다. 그렇기 때문에 우리는 Model의 input으로 들어온 이미지의 Neighbor들의 Caption 정보를 토대로 Attribute를 얻어낼 수 있다. 구체적으로는 다음과 같은 순서로 알고리즘을 진행한다.
- GoogleNet feature를 이용하여 Input 이미지와 large-scale data들 간의 거리를 구한다.
- Input Image와 거리가 가장 가까운 K개의 이미지를 뽑는다.(K-Neareat Neighbor)
- 2에서 뽑은 K개의 이미지들의 Caption에서 가장 많이 등장하는 N개의 단어를 뽑는다.(Term-Frequency)
- 이 N개의 단어들을 Attribute로 이용한다.
2. Parametric attribute prediction
이 방법은 사실 쉽게 말하면 Multi-label Classifier와 다를 것이 없다. 즉 Train data로부터 먼저 가장 많이 등장하는 단어들을 모아서 category화 시키고, 이미지를 Network에 넣어서 각 Class에 대한 score를 얻은 뒤, score가 가장 높은 몇 개의 단어들을 Attribute로 이용한다. 구체적으로는 다음과 같은 순서로 알고리즘을 진행한다.
- Train Data에 가장 많이 등장하는 K개의 단어들을 골라서 K개의 Class를 형성한다.
- 위의 K 개의 단어 중 N개를 뽑아 Attribute로 사용한다. 그 방법에는 두 가지가 있다.
2-1. Multi-label Classifier를 이용하여 K개의 단어 중 한 개가 아닌 N 개의 Class를 한번에 뽑는다.
2-2. FCN(Fully Convolutional Network)를 이용하여 각 Patch 별로 K-Class Classification을 진행한다. - 이렇게 얻은 N개의 단어를 Attribute로 이용한다.