안녕하세요. 오늘은 Deep Residual Learning, Guided Filtering, Faster R-CNN 등으로 유명한 Kaiming He의 CVPR 논문인 [Single Image Haze Reduction Removal Using Dark Channel Prior]에 대한 리뷰를 하려고 합니다. 아이디어도 대단하지만 논문이 매우 논리적이고 쉽게 구성되어 있어, 논문을 처음 접하시는 분들 께서도 비교적 쉽게 읽어나갈 수 있으니 원문도 한 번 읽어보시기를 추천드립니다.
Abstract

이 논문은 ‘Dark Channel Prior’를 이용하여 Single Image에 존재하는 Haze(그림1.(a)와 같이 대상 물체와 관찰자 사이에 존재하는 물질들에 의해 빛이 진행을 방해받아 대상이 뿌옇게 보이는 현상)를 제거하는 알고리즘을 제안하는 논문이다.
‘Dark Channel Prior’의 Prior는 흔히 ‘사전 지식’이라는 의미로 논문에서 쓰이게 되는데, 본 논문에서 쓰인 의미를 간단히 풀어서 쓰면 ‘사람이 관찰을 통해 얻어낸 사전 지식’이라는 뜻으로 보면 된다. 이 논문에서는 ‘Haze가 존재하지 않는 픽셀’들은 대부분 R,G,B 세 채널 중에서 적어도 한 채널의 명도 값이 매우 낮은 경향을 갖는다는 사실을 발견하였다고 한다. 이 채널을 ‘Dark Channel’이라고 정의하고 이러한 사실을 ‘Dark Channel Prior’라고 지칭한다.
본 논문에서는 이러한 Dark Channel Prior를 이용하여 다양한 아웃도어 이미지들에 존재하는 Haze를 제거한다. 또한 이렇게 Haze를 제거하는 과정에서 생긴 부산물로서 Depth Map을 얻을 수도 있게 된다.
Backgrougnd
Haze는 어떻게 형성될까?
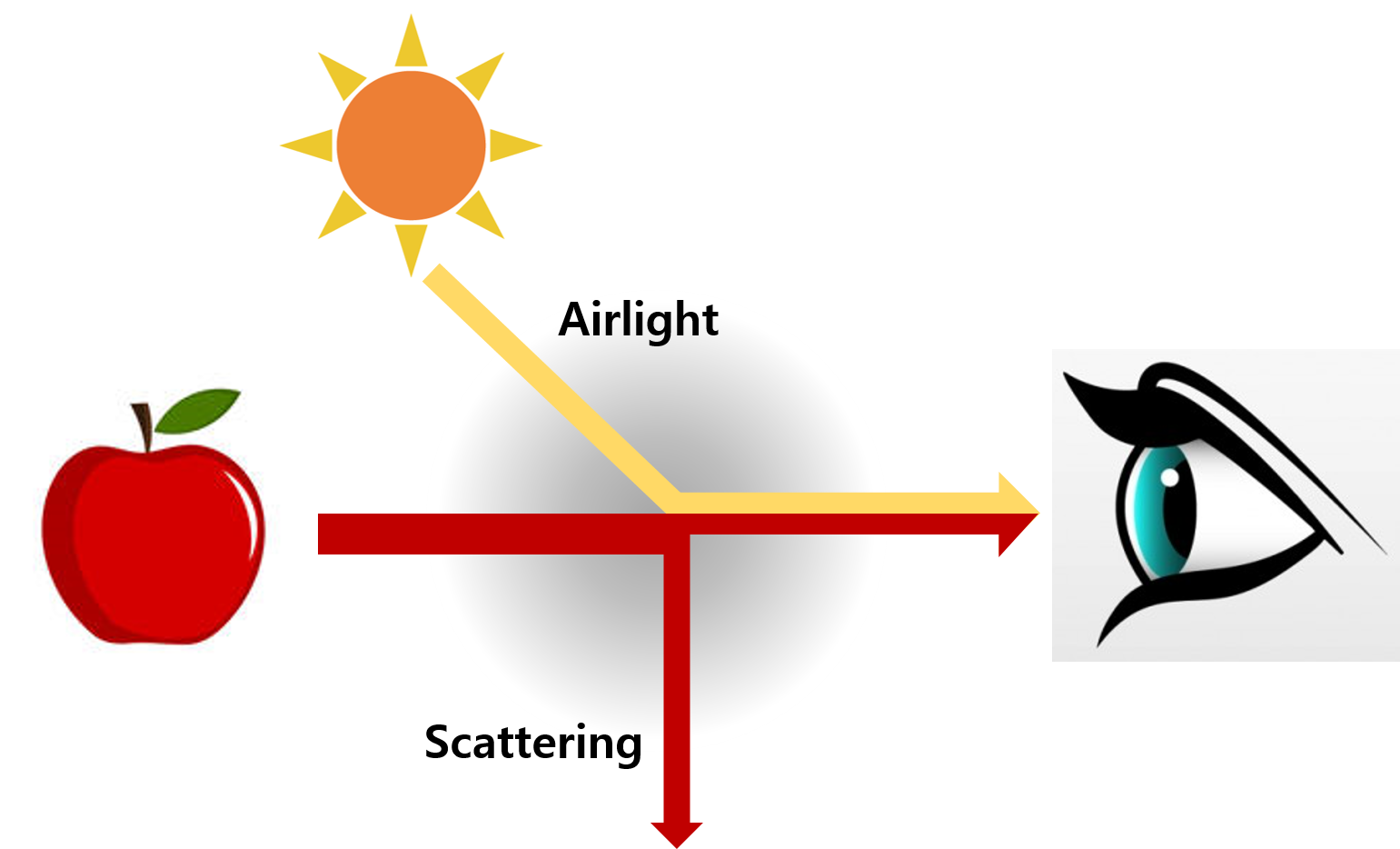
Haze는 기본적으로 그림 2와 같이 물체로부터 반사된 후 대기에 의해 일부 손실된 빛과 태양 등 주변 광원으로부터 대기에 반사되어 함께 시야에 들어오는 대기 산란광(Airlight)이 섞임으로 인해 발생한다. 즉 대상이 뿌옇게 보이는 이유는 대기로 인해 우리가 원하는 빛이 손실됨과 동시에 주변 광원으로 인해 우리가 원하지 않는 빛이 함께 우리 눈에 도달하기 때문이다. 이는 식으로 다음과 같이 표현할 수 있다.
$$I(x) = J(x)t(x) + A(1-t(x))$$
$x$ : 2차원 벡터로, 각 픽셀의 위치를 의미.
$J(x)$ : Haze에 의해 왜곡되기 이전의 이미지.
$I(x)$ : 실제 카메라에 찍히는 이미지. 즉 Haze에 왜곡된 이미지.
$t(x)$ : 대기 투과율(Medium Transmission). 대기를 거쳐 최종적으로 관찰자에게 도달하는 빛의 비율. 0과 1 사이의 값을 갖는다.
$A$ : 대기 산란광(Airlight). 이 값은 모든 픽셀에 같은 값이 들어간다고 가정한다.
식을 해석해보면, 대상으로부터 반사된 신호($J(x)$)는 대기를 통과하면서 일부가 손실되고, $J(x)t(x)$만큼의 신호만 남게 된다. 또한 태양을 비롯한 주변 광원에 의해 형성된 Airlight($A$)가 이 신호에 일부 섞이게 되면서 최종적으로 $I(x)$가 형성되어 관찰자에게 도달하게 된다.
Object와 관찰자 사이의 거리가 멀수록 그 사이에는 더 두꺼운 대기층이 존재하게 되고, 이로 인해 Haze는 더 심해지게 된다. 즉 거리가 멀수록 Haze가 심하다. 이런 성질로부터 $t(x)$는 다음과 같이 정의된다.
$$t(x) = e^{-\beta d(x)}$$
$\beta$ : 산란 계수(Scattering Coefficient).
$d(x)$ : 픽셀 $x$에서의 대상과 관찰자와의 거리(Depth).
이 식에 의해 Haze는 대상과의 거리가 멀수록 강해지게 되며, 멀리 있는 산이 가까이 있는 산보다 흐리게 보이는 등, 일상생활에서도 이러한 현상을 자주 경험할 수 있다. 미술 용어로 이를 대기 원근법(Aerial Perspective) 이라고도 한다.
Haze의 정체를 알아봤으니, 다시 식으로 돌아가서, 원본 영상을 복원해 내는 방법을 생각해보도록 하자.
$$I(x) = J(x)t(x) + A(1-t(x))$$
우리는 위 식으로부터 $J(x)$와 $t(x)$를 전부 구해 내야 한다($A$는 일단은 주어진 값이라고 가정하자). $J(x)$는 우리가 최종적으로 얻고 싶은 대상이므로 $t(x)$를 먼저 구하고, 이를 바탕으로 $J(x)$를 구하는 방향으로 문제를 풀어나갈 것이다.
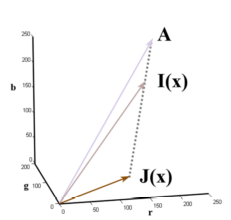
먼저, 헷갈리지 않기 위해 $I(x)$, $J(x)$, $t(x)$의 정체를 확실히 하고 넘어가자. $x$는 고정된 점이므로 $I(x)$와 $J(x)$는 r,g,b 세 값을 성분으로 갖는 3차원 벡터이다. 그리고 $t(x)$는 단순히 대기를 통과하는 빛의 비율 값이므로 스칼라 값이다.
이제 위 식을 잘 살펴보자. 식의 꼴을 살펴보면 내분점 공식이라는 사실을 알 수 있다. 즉 $I(x)$는 그림 3과 같이 3차원 공간 상에서 $J(x)$와 $A$를 연결하는 선분 위의 점일 뿐만 아니라, $J(x)$와 $A$ 사이를 $(1-t(x)) : t(x)$로 내분하는 내분점이다. 그렇기 때문에 다음과 같이 길이 비교를 통해 쉽게 $t(x)$의 값을 얻을 수 있다.
$$t(x) = \frac{||A-I(x)||}{||A-J(x)||}$$
또한 이상적인 상황을 가정하면, r,g,b 채널 모두 대기를 통과하면서 같은 비율로 손실 될 것이므로 $t(x)$는 모든 Channel에 대해 같은 값일 것이다. 그렇기 때문에 특정 Channel $c$에 대하여 다음과 같이 식을 쓸 수 있게 된다.
$$t(x) = \frac{||A-I(x)||}{||A-J(x)||} = \frac{A^c-I^c(x)}{A^c-J^c(x)}$$
하지만 결과적으로 이 정보만으로는 $t(x)$를 구할 수 없다. 미지수인 $J(x)$가 식에 포함되어 있기 때문이다. 사실 그도 그럴 것이, 알고자 하는 값이 2개인데 활용 가능한 정보는 식 하나 밖에 없었으므로 당연한 결과이다. 정보가 하나 더 필요한 상황이다. 이 때, 특정 $c$에 대해서 $J^c(x)$를 우리가 알 수 있다면?
이 정보가 바로 Dark Channel Prior이며, 다음과 그 다음 Chapter를 통해 Dark Channel Prior를 식에 적용해보도록 할 것이다.
Dark Channel Prior
이 논문에서는 ‘Haze가 존재하지 않는 픽셀’들은 대부분 R,G,B 세 채널 중에서 적어도 한 채널의 명도 값이 매우 낮은 경향을 갖는다는 사실을 발견하였다고 한다. 이 채널을 ‘Dark Channel’이라고 정의하고 이러한 사실을 ‘Dark Channel Prior’라고 지칭한다. 임의의 이미지 $J$에 대하여 이렇게 정의된 Dark Channel을 수식을 통해 나타내면 다음과 같다.
$$J^{dark}(x) = \min _{c \in \{r,g,b\} }( \min _{y \in \Omega (x)}(J^c(y)))$$
$J^{dark}(x)$ : Dark Channel.
$J^c(x)$ : 픽셀 $x$의 r,g,b중 한 Channel을 의미.
$\Omega (x)$ : $x$를 중심으로 하는 일정 범위 안의 Pixel들의 집합. $x$ 주변의 Pixel들의 집합(Local Patch).
식을 해석해보면, 특정 Pixel $x$에 해당하는 Dark Channel 값은, $x$주변의 픽셀들이 가지고 있는 모든 Channel 값들 중에서 가장 작은 값이 된다. $J^{dark}(x)$ 값이 작게 나오는 픽셀은 대부분 다음 세 경우 중 하나에 해당한다.
- 건물이나 다른 구조물 등에 의해 생긴 그림자 영역인 경우
- Colorful한 Object나 Surface. 보통 Haze가 강한 경우에는 불가능하다.
- 검은색 또는 어두운 색의 Object나 Surface.
보통 Haze가 존재하지 않는 아웃도어 이미지는 Colorful하거나 어두운 색의 대상들 또는 그들의 그림자로 가득 차 있기 때문에, Dark Pixel 값이 작게 나온다(단, 이미지에 하늘이 있을 경우 하늘 영역에 한해서만 Haze가 없음에도 불구하고 Dark Pixel 값이 크게 나오는데, 이는 뒤에서 해결할 것이다.). 반면 Haze가 강한 이미지는 이러한 대상들이 뿌옇고 잘 보이지 않게 되므로 Dark Pixel 값이 크게 나온다. 이러한 사실을 기반으로 우리는 이미지로부터 Haze를 분리해 낼 수 있게 된다. 그림 4를 보면 알 수 있듯이, 이러한 Dark Channel Prior는 굉장히 잘 적용된다.

오른쪽: Haze가 존재하는 이미지와 이에 해당하는 Dark Channel 이미지. (출처: 본 논문)
Haze Removal Using Dark Channel Prior
1. Estimating the Transmission
이제 Dark Channel Prior를 적용하여 $t(x)$를 구하고 이를 통해 최종적으로 $J(x)$를 구할 것이다. 구하기 전에, 편의를 위해 다음 두가지를 가정하고 넘어갈 것이다.
- Loacl Patch $\Omega (x)$ 안에 속한 픽셀들의 $t(x)$ 값들은 근사적으로 $\tilde t(x)$로 동일하다고 가정한다.
- Dark Channel Prior에 따라 Haze가 존재하지 않는 픽셀의 세 Channel 중 적어도 하나의 값은 매우 작은데, 이 값을 0이라고 가정한다.
추가적으로, 위에서도 언급한 바 있듯이 $A$의 값은 일단 주어진 값으로 취급하고, 뒤에서 따로 구할 것이다. 먼저 Local Patch $\Omega (x)$에서 특정 Channel $c$에 대하여 Haze 식을 작성해보면 다음과 같을 것이다.
$$I^c(x) = J^c(x){\tilde t(x)} + A^c(1-{\tilde t(x)})$$
이제 Dark Channel Prior를 적용하기 위해 양 변에 각 Patch에 대한 Minimun Operation을 취하도록 하자.
$$\min_ {y \in \Omega (x)}(I^c(y)) = \min_ {y \in \Omega (x)}(J^c(y){\tilde t(x)}) + A^c(1-{\tilde t(x)})$$
$A$는 모든 픽셀에 대해 동일하고, $\tilde t(x)$는 각 Local Patch에 대해 동일하다고 하였으므로,
$$\min_ {y \in \Omega (x)}(\frac {I^c(y)}{A^c}) = {\tilde t(x)} \min_ {y \in \Omega (x)}(\frac {J^c(y)}{A^c}) + (1-{\tilde t(x)})$$
Dark Channel은 세 Channel중 가장 값이 작은 Channel을 의미하므로 $c$에 대한 Minimum Operation을 취하도록 하자.
$$\min_ c (\min_ {y \in \Omega (x)}(\frac {I^c(y)}{A^c})) = {\tilde t(x)} \min_ c (\min_ {y \in \Omega (x)}(\frac {J^c(y)}{A^c})) + (1-{\tilde t(x)})$$
이 때, Dark Channel Priority에 따르면
$$J^{dark}(x) = \min_ c (\min_ {y \in \Omega (x)}(J^c(y))) = 0$$
이 성립하므로, 식은 다음과 같이 정리된다.
$$\tilde t(x) = 1 - \min_ c (\min_ {y \in \Omega (x)}(\frac {I^c(y)}{A^c}))$$
이로써 우리는 $\tilde t(x)$를 구하게 되었다. 이제 앞에서 언급한 하늘 영역에서 Dark Channel 값이 크게 나오는 현상을 잠깐 짚고 넘어가자. Haze 이미지에서 하늘은 대기에 존재하는 빛, 즉 $A$와 유사한 색을 갖게 되는데, 이로부터 다음 식이 성립하게 된다.
$$\min_ c (\min_ {y \in \Omega (x)}(\frac {I^c(y)}{A^c})) \rightarrow 1, and \space\space\space \tilde t(x) \rightarrow 0$$
하늘이 무한히 먼 거리에 존재한다는 점을 생각했을 때, 위 식은 거리에 따른 투과율 함수 $t(x) = e^{-\beta d(x)}$에 잘 부합하게 된다. 그렇기 때문에 우리는 하늘 영역에 대해 특별히 구분해서 생각해 줄 필요 없이 그대로 위에 제시된 모델을 이용하면 된다는 결론을 얻는다.
이제 $\tilde t(x)$를 이용하여 $J(x)$를 구하게 될텐데, $\tilde t(x)$를 그대로 사용하기에는 몇 가지 문제가 존재한다. 그렇기 때문에 이를 해결하기 위해 몇 가지 작업이 추가적으로 필요하다.
첫 번째로, 아무리 날이 맑아도 대기중에는 항상 대기 입자들이 존재한다. 그렇기 때문에 우리가 먼 지점을 보게 되면 그 사이에는 여전히 빛의 진행을 방해하는 입자들이 존재하게 된다. 심지어는 이러한 이유 때문에 대상 물체를 봤을 때 사람이 느끼는 Haze는 대상과 자신 사이의 거리를 가늠하는 한 척도가 된다(위에서 언급했듯이 이것을 대기 원근법이라고 한다). 간단히 말하면, 멀리 있는 물체마저도 Haze가 완벽히 제거된 이미지는 사람이 봤을 때 자연스럽지 못하다. 그렇기 때문에 우리는 매우 약간의 Haze를 제거하지 않고 남겨두기 위해 $\tilde t(x)$를 고평가할 필요가 있다. 즉 실제보다 $\tilde t(x)$를 높게 평가 하여, Haze를 제거하는 정도를 살짝 낮추는 것이다. 그래서 우리는 $\omega (0< \omega \leq 1)$를 도입하여 위 식을 약간 수정한다. 본 논문에서는 $\omega$값으로 0.95를 썼다고 한다.
$$\tilde t(x) = 1 - \omega \min_ c (\min_ {y \in \Omega (x)}(\frac {I^c(y)}{A^c}))$$
두 번째로, 본 논문에서는 Local Patch $\Omega (x)$의 사이즈를 $15 \times 15$로 설정하였는데, 이로 인해 얻은 transmission map($\tilde t(x)$의 각 픽셀을 이미지로 나타낸 Map)은 그림 5의 (b)와 같이 Block 효과가 발생하여 디테일한 부분이 제대로 표현되지 않는 문제가 발생한다. 그렇기 때문에 우리가 얻은 $\tilde t(x)$는 사용되기 전에 Soft Matting이라는 처리 과정을 거치게 된다.

2. Soft Matting
Dark Channel Prior를 통해 얻은 Transmission Map은 Local Patch를 이용하기 때문에 block 현상이 발생한다. 이를 해결하기 위해 Soft Matting 논문에 소개된 Closed Form Solution을 이용하는데, 자세한 설명은 이 논문을 참고하길 바란다. Soft Matting 알고리즘을 이용하면, 다음 식을 minimize함으로 인해 $t(x)$를 수정할 수 있다고 한다.
$$E(t) = t^TLt + \lambda (t - \tilde t)^T(t - \tilde t)$$
$$L = \sum _{k|(i,j) \in w_k} (\delta _{ij} - \frac {1}{|w_k|}(1 + (I_i - \mu _k)^T(\Sigma _k + \frac {\epsilon}{|w_k|} U_3)^{-1}(I_j - \mu _k))) $$
$\lambda$ : regularization parameter.
$w_k$ : $k$번째 window.
$I_i$ : Pixel $i$에서의 Image Color.
$\delta _{ij}$ : Kronecker delta.
$\mu _k$ : $w_k$의 픽셀 값들의 평균.
$\Sigma _k$ : $w_k$의 픽셀 값들의 Covariance Matrix.
$U _n$ : $n \times n$ Identity Matrix.
그리고 위 식을 minimize한 결과의 closed form solution이 존재하는데, 다음과 같다.
$$(L + \lambda U)t = \lambda \tilde t$$
본 논문에서는 $\lambda$ 값으로 $10^{-4}$을 썼고, 이를 통해 구한 $t(x)$가 비로소 우리가 $J(x)$를 구하는데 쓸 수 있는 Transmission이 된다. Soft Matting을 통해 얻은 $t(x)$에 해당하는 transmission map은 그림 5의 (c)와 같다.
3. Recovering the Scene Radiance
이제, 우리는 $t(x)$를 구했기 때문에 간단히 $I(x) = J(x)t(x) + A(1-t(x))$로부터 $J(x)$를 구할 수 있다.
$$J(x) = \frac {I(x)-A}{t(x)} + A$$
하지만 $t(x)$가 0에 매우 가까운 경우, $J(x)$의 값이 불안정하여 noise가 생기는 경향이 있는데, 이를 방지하기 위해서 lower bound $t_0(=0.1)$를 두어 clip한다. 그러므로 최종적인 식은 다음과 같다.
$$J(x) = \frac {I(x)-A}{\max (t(x),t_0)} + A$$
이를 통해 우리는 그림 5의 (d)와 같이 Haze가 제거된 이미지를 얻을 수 있다.
4. Estimating the Atmospheric Light & Depth map
Haze Removal이 전부 완료된 것 처럼 보이지만, 우리에게는 할 일이 한 가지 더 남아 있다. 바로 Airlight $A$를 구하는 것이다. 또한 논문에는 Depth Map 추정 부분이 Experiment에 빠져 있지만, 양이 적어 한꺼번에 소개하려고 한다.

먼저, $A$ 값으로 가장 적당한 값은 이미지 전체에서 Haze가 가장 강한 픽셀의 값이 될 것이다. 그래서 대부분의 Haze Removal 논문에서는 $A$ 값으로 간단히 이미지 전체에서 가장 밝은 픽셀을 사용하였다. 하지만 이는 흰 색의 차 또는 건물과 Haze를 구분할 수 없다는 단점을 지닌다. 그렇기 때문에 여기서 또 한번 Dark Channel이 이용된다. 먼저 Dark Pixel 이미지를 얻은 후, 그림 6의 노란색 테두리 부분과 같이 이미지 상에서 밝기가 상위 0.1% 안에 드는 픽셀들을 뽑는다. 이 픽셀들은 Haze가 강한 픽셀일 확률이 매우 높기 때문에, 이 픽셀들 중 원본 이미지에서 가장 밝은 픽셀 값을 $A$ 값으로 쓴다.
또한 Abstract에서도 설명했듯이, 우리는 Haze Removal의 부산물로서 Depth Map을 쉽게 얻을 수 있는데, 다음 식을 이용하면 된다.
$$t(x) = e^{-\beta d(x)}$$
$$\therefore d(x) = -\frac {1}{\beta} \ln(t(x))$$
이 식을 통해 우리는 최종적으로 Depth Map까지 얻을 수 있게 된다.
아래 그림들은 본 논문에서 제안하는 알고리즘을 이용하여 Haze를 제거한 결과와, 그 과정에서 얻은 Depth Map의 결과이다.

Conclusion
본 논문의 알고리즘은 Single Image만으로 성공적으로 Haze가 제거된 영상 뿐만아니라 Depth Map까지 얻을 수 있다. 하지만 몇 가지 한계점들이 있는데, 다음과 같다.
- 다양한 이미지들을 보고 통계적으로 얻은 Prior를 이용하기 때문에 특정 이미지들에 대해서는 잘 적용되지 않을 수 있다.
- Object가 대기상의 빛과 비슷한 색을 띠는 물체인데, 그림자마저 드리워지지 않은 상황이라면 Haze로 취급될 수 있다.
- 대부분의 Haze 알고리즘들이 그렇듯, Haze 제거 알고리즘 모델 자체가 논리적 근거가 다소 빈약하다는 점이 있다. 즉 Haze에 의해 발생하는 현상들만을 근거로 하고 있을 뿐, 이러한 현상들이 왜 발생하는지 등에 대한 심층적인 분석이 부족하다.